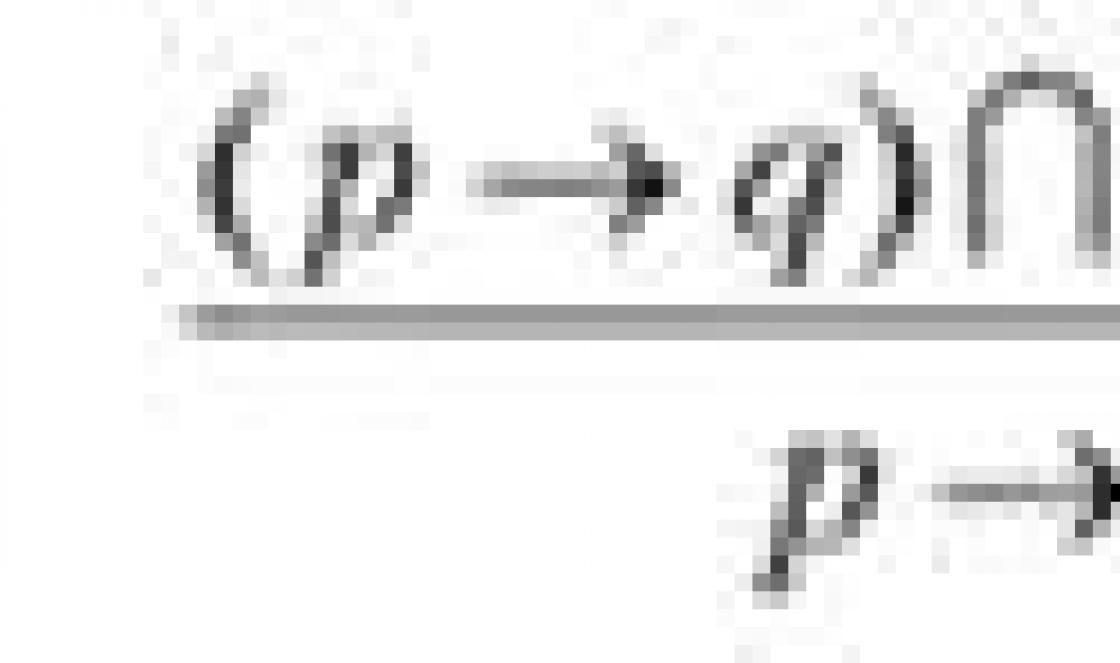Ci sono alcune regole per confrontare i numeri. Considera il seguente esempio.

Ieri il termometro indicava 15°C e oggi indica 20°C. Oggi fa più caldo di ieri. Il numero 15 è minore del numero 20, possiamo scriverlo così: 15< 20. А, если мы представим эти числа на координатной прямой, то точка со значением 15 будет расположена левее точки со значением 20.

Consideriamo ora le temperature negative. Ieri c'era -12˚ C, e oggi -8˚ C. Oggi fa più caldo di ieri. Pertanto, considera che il numero -12 è inferiore al numero -8. Sulla linea delle coordinate orizzontali, il punto con valore -12 si trova a sinistra del punto con valore -8. Possiamo scriverlo così: -12< -8.

Quindi, se confrontiamo i numeri usando una linea di coordinate orizzontale, dei due numeri, quello più piccolo è quello la cui immagine sulla linea di coordinate si trova a sinistra, e quello più grande è quello la cui immagine si trova a destra. Ad esempio, abbiamo A > B e C nella figura, ma B > C.

Sulla linea delle coordinate, i numeri positivi si trovano a destra di zero e i numeri negativi a sinistra di zero, ogni numero positivo è maggiore di zero e ogni negativo è minore di zero, quindi ogni numero negativo è minore di ogni numero positivo.

Quindi, la prima cosa a cui devi prestare attenzione quando confronti i numeri sono i segni dei numeri confrontati. Un numero con un meno (negativo) è sempre minore di uno positivo.

Se confrontiamo due numeri negativi, dobbiamo confrontare i loro moduli: il numero con il modulo inferiore sarà maggiore e il numero con il modulo inferiore sarà inferiore. Ad esempio, -7 e -5. I numeri confrontati sono negativi. Confronta i loro moduli 5 e 7. 7 è maggiore di 5, quindi -7 è inferiore a -5. Se segniamo due numeri negativi sulla linea delle coordinate, il numero più piccolo sarà a sinistra e quello più grande a destra. -7 si trova a sinistra di -5, quindi -7< -5.

Confronto di frazioni ordinarie

Di due frazioni con lo stesso denominatore, quella con il numeratore più piccolo è la più piccola e quella con il numeratore più grande è la più grande.

Puoi confrontare solo frazioni con lo stesso denominatore.

Algoritmo per confrontare frazioni ordinarie

1) Se la frazione ha una parte intera, iniziamo il confronto con essa. La frazione maggiore è quella con la parte intera maggiore. Se le frazioni non hanno una parte intera o sono uguali, vai al passaggio successivo.

2) Se le frazioni con denominatore diverso devono essere ricondotte a un denominatore comune.

3) Confronta i numeratori delle frazioni. La frazione più grande è quella con il numeratore più grande.

Si noti che una frazione con una parte intera sarà sempre maggiore di una frazione senza una parte intera.

Confronto decimale

I decimali possono essere confrontati solo con lo stesso numero di cifre (cifre) a destra del punto decimale.

Algoritmo di confronto decimale

1) Prestare attenzione al numero di caratteri a destra della virgola. Se il numero di cifre è lo stesso, possiamo iniziare a confrontare. In caso contrario, aggiungere il numero richiesto di zeri in una delle frazioni decimali.

2) Confronta i decimali da sinistra a destra: interi con interi, decimi con decimi, centesimi con centesimi, ecc.

3) La frazione maggiore sarà quella in cui una delle parti è maggiore dell'altra frazione (iniziamo il confronto con gli interi: se la parte intera di una frazione è maggiore, allora l'intera frazione è maggiore).

Ad esempio, confrontiamo i decimali:

1) Aggiungere il numero di zeri richiesto nella prima frazione per equalizzare il numero di cifre decimali

57.300 e 57.321

2) Iniziamo a confrontare da sinistra a destra:

interi con interi: 57 = 57;

decimi con decimi: 3 = 3;

centesimi con centesimi: 0< 2.

Poiché i centesimi della prima frazione decimale sono risultati inferiori, l'intera frazione sarà inferiore:

57,300 < 57,321

sito, con copia integrale o parziale del materiale, è richiesto un link alla fonte.

Il confronto dei numeri è uno degli argomenti più facili e divertenti in un corso di matematica. Tuttavia, va detto che non è così semplice. Ad esempio, poche persone hanno difficoltà a confrontare numeri positivi a una o due cifre.

Ma i numeri con un gran numero di segni causano già problemi, spesso le persone si perdono quando confrontano numeri negativi e non ricordano come confrontare due numeri con segni diversi. Cercheremo di rispondere a tutte queste domande.

Regole per confrontare i numeri positivi

Iniziamo con il più semplice: con numeri che non hanno alcun segno davanti a loro, cioè con quelli positivi.

• Innanzitutto vale la pena ricordare che tutti i numeri positivi sono, per definizione, maggiori di zero, anche se noi stiamo parlando su un numero frazionario senza numero intero. Ad esempio, la frazione decimale 0,2 sarà maggiore di zero, poiché sulla linea delle coordinate il punto corrispondente è ancora a due piccole divisioni da zero.
• Se stiamo parlando di confrontare due numeri positivi con un numero elevato di caratteri, è necessario confrontare ciascuna delle cifre. Ad esempio, 32 e 33. La cifra delle decine per questi numeri è la stessa, ma il numero 33 è più grande, perché nelle unità la cifra "3" è maggiore di "2".
• Come si confrontano due decimali? Qui devi prima guardare la parte intera, ad esempio una frazione di 3,5 sarà inferiore a 4,6. Cosa succede se la parte intera è la stessa, ma le cifre decimali sono diverse? In questo caso, si applica la regola per gli interi: è necessario confrontare i segni con le cifre fino a trovare decimi, centesimi, millesimi sempre più piccoli. Ad esempio, 4,86 ​​è maggiore di 4,75 perché otto decimi è maggiore di sette.

Confronto di numeri negativi

Se abbiamo alcuni numeri -a e -c nel problema e dobbiamo determinare quale di essi è maggiore, allora si applica la regola universale. Per prima cosa, i moduli di questi numeri vengono scritti - |a| e |c| - e vengono confrontati tra loro. Il numero il cui modulo è maggiore sarà minore rispetto ai numeri negativi e viceversa: il numero maggiore sarà quello il cui modulo è minore.

Cosa succede se devi confrontare un numero negativo e uno positivo?

Qui funziona solo una regola, ed è elementare. I numeri positivi sono sempre maggiori dei numeri con il segno meno, qualunque essi siano. Ad esempio, il numero "1" sarà sempre maggiore del numero "-1458" semplicemente perché l'unità si trova a destra di zero sulla linea delle coordinate.

Devi anche ricordare che qualsiasi numero negativo è sempre inferiore a zero.

Continuiamo a studiare i numeri razionali. In questa lezione impareremo a confrontarli.

Dalle lezioni precedenti, abbiamo appreso che più a destra si trova il numero sulla linea delle coordinate, più è grande. E di conseguenza, più a sinistra si trova il numero sulla linea delle coordinate, più è piccolo.

Ad esempio, se confronti i numeri 4 e 1, puoi immediatamente rispondere che 4 è maggiore di 1. Questa è un'affermazione completamente logica e tutti saranno d'accordo con questo.

La dimostrazione è la linea delle coordinate. Mostra che i quattro si trovano a destra dell'unità

Per questo caso, c'è una regola che puoi usare se lo desideri. Si presenta così:

Di due numeri positivi, il numero con il modulo maggiore è maggiore.

Per rispondere alla domanda quale numero è più grande e quale è più piccolo, devi prima trovare i moduli di questi numeri, confrontare questi moduli e quindi rispondere alla domanda.

Ad esempio, confrontiamo gli stessi numeri 4 e 1 applicando la regola precedente

Trova moduli di numeri:

|4| = 4

|1| = 1

Confronta i moduli trovati:

4 > 1

Rispondiamo alla domanda:

4 > 1

Per i numeri negativi, c'è un'altra regola, simile a questa:

Di due numeri negativi, quello il cui modulo è minore è maggiore.

Ad esempio, confrontiamo i numeri −3 e −1

Trova moduli di numeri

|−3| = 3

|−1| = 1

Confronta i moduli trovati:

3 > 1

Rispondiamo alla domanda:

−3 < −1

Non confondere il modulo di un numero con il numero stesso. Un errore comune a molti neofiti. Ad esempio, se il modulo del numero −3 è maggiore del modulo del numero −1, ciò non significa che il numero −3 sia maggiore del numero −1.

Il numero -3 è minore del numero -1. Questo può essere compreso usando la linea delle coordinate

Si può vedere che il numero -3 si trova più a sinistra di -1. E sappiamo che più ci si sposta a sinistra, meno è.

Se confronti un numero negativo con uno positivo, la risposta si suggerirà da sola. Qualsiasi numero negativo sarà inferiore a qualsiasi numero positivo. Ad esempio, −4 è minore di 2

Si può vedere che -4 si trova più a sinistra di 2. E sappiamo che "più è a sinistra, meno è".

Qui, prima di tutto, devi guardare i segni dei numeri. Un meno davanti a un numero indicherà che il numero è negativo. Se non c'è alcun segno del numero, allora il numero è positivo, ma puoi scriverlo per chiarezza. Ricordiamo che questo è un segno più

Abbiamo considerato come esempio interi della forma -4, -3 -1, 2. Non è difficile confrontare tali numeri, nonché rappresentarli su una linea di coordinate.

È molto più difficile confrontare altri tipi di numeri, come frazioni, numeri misti e decimali, alcuni dei quali sono negativi. Qui, principalmente, dovrai applicare le regole, perché non è sempre possibile rappresentare con precisione tali numeri sulla linea delle coordinate. In alcuni casi, il numero sarà necessario per facilitare il confronto e la comprensione.

Esempio 1 Confronta i numeri razionali

Quindi, è necessario confrontare un numero negativo con uno positivo. Qualsiasi numero negativo è minore di qualsiasi numero positivo. Pertanto, senza perdere tempo, rispondiamo che è inferiore a

Esempio 2

Vuoi confrontare due numeri negativi. Di due numeri negativi, il maggiore è quello il cui modulo è minore.

Trova moduli di numeri:

Confronta i moduli trovati:

Esempio 3 Confronta i numeri 2.34 e

Vuoi confrontare un numero positivo con uno negativo. Qualsiasi numero positivo è maggiore di qualsiasi numero negativo. Pertanto, senza perdere tempo, rispondiamo che 2,34 è maggiore di

Esempio 4 Confronta i numeri razionali e

Trova moduli di numeri:

Confronta i moduli trovati. Ma prima, portiamoli in una forma comprensibile, in modo che sia più facile confrontarli, ovvero tradurli in frazioni improprie e portarli a un denominatore comune

Secondo la regola, di due numeri negativi, maggiore è il numero il cui modulo è minore. Quindi il razionale è maggiore di perché il modulo del numero è minore del modulo del numero

Esempio 5

Vuoi confrontare zero con un numero negativo. Zero è maggiore di qualsiasi numero negativo, quindi senza perdere tempo rispondiamo che 0 è maggiore di

Esempio 6 Confronta i numeri razionali 0 e

È necessario confrontare lo zero con un numero positivo. Zero è minore di qualsiasi numero positivo, quindi senza perdere tempo rispondiamo che 0 è minore di

Esempio 7. Confronta i numeri razionali 4.53 e 4.403

È necessario confrontare due numeri positivi. Di due numeri positivi, il numero con il modulo maggiore è maggiore.

Facciamo in modo che il numero di cifre dopo la virgola decimale sia lo stesso in entrambe le frazioni. Per fare ciò, nella frazione 4.53, aggiungi uno zero alla fine

Trova moduli di numeri

Confronta i moduli trovati:

Secondo la regola, di due numeri positivi, il numero maggiore è quello il cui modulo è maggiore. Quindi il numero razionale 4.53 è maggiore di 4.403 perché il modulo di 4.53 è maggiore del modulo di 4.403

Esempio 8 Confronta i numeri razionali e

Vuoi confrontare due numeri negativi. Di due numeri negativi, quello il cui modulo è minore è maggiore.

Trova moduli di numeri:

Confronta i moduli trovati. Ma prima, portiamoli a una forma comprensibile per rendere più facile il confronto, vale a dire, tradurremo il numero misto in una frazione impropria, quindi porteremo entrambe le frazioni a un denominatore comune:

Secondo la regola, di due numeri negativi, maggiore è il numero il cui modulo è minore. Quindi il razionale è maggiore di perché il modulo del numero è minore del modulo del numero

Confrontare i decimali è molto più semplice che confrontare frazioni comuni e numeri misti. In alcuni casi, guardando la parte intera di tale frazione, puoi rispondere immediatamente alla domanda su quale frazione è maggiore e quale minore.

Per fare ciò, è necessario confrontare i moduli di parti intere. Ciò ti consentirà di rispondere rapidamente alla domanda nel problema. Dopotutto, come sai, le parti intere nelle frazioni decimali hanno un peso maggiore di quelle frazionarie.

Esempio 9 Confronta i numeri razionali 15.4 e 2.1256

Il modulo della parte intera della frazione 15.4 è maggiore del modulo della parte intera della frazione 2.1256

quindi la frazione 15,4 è maggiore della frazione 2,1256

15,4 > 2,1256

In altre parole, non abbiamo dovuto perdere tempo ad aggiungere zeri alla frazione 15,4 e confrontare le frazioni risultanti come numeri ordinari.

154000 > 21256

Le regole di confronto rimangono le stesse. Nel nostro caso, abbiamo confrontato numeri positivi.

Esempio 10 Confronta i numeri razionali −15,2 e −0,152

Vuoi confrontare due numeri negativi. Di due numeri negativi, quello il cui modulo è minore è maggiore. Ma confronteremo solo moduli di parti intere

Vediamo che il modulo della parte intera della frazione −15,2 è maggiore del modulo della parte intera della frazione −0,152.

Ciò significa che il razionale −0.152 è maggiore di −15.2 perché il modulo della parte intera di −0.152 è minore del modulo della parte intera di −15.2

−0,152 > −15,2

Esempio 11. Confronta i numeri razionali −3.4 e −3.7

Vuoi confrontare due numeri negativi. Di due numeri negativi, quello il cui modulo è minore è maggiore. Ma confronteremo solo moduli di parti intere. Ma il problema è che i moduli degli interi sono uguali:

In questo caso, dovrai usare il vecchio metodo: trova i moduli dei numeri razionali e confronta questi moduli

Confronta i moduli trovati:

Secondo la regola, di due numeri negativi, maggiore è il numero il cui modulo è minore. Quindi il razionale −3.4 è maggiore di −3.7 perché il modulo di −3.4 è minore del modulo di −3.7

−3,4 > −3,7

Esempio 12. Confronta i numeri razionali 0,(3) e

È necessario confrontare due numeri positivi. E confronta una frazione periodica con una frazione semplice.

Traduciamo la frazione periodica 0, (3) in una frazione ordinaria e confrontiamola con la frazione . Dopo aver convertito la frazione periodica 0, (3) in una frazione ordinaria, si trasforma in una frazione

Trova moduli di numeri:

Confronta i moduli trovati. Ma prima, portiamoli a una forma comprensibile, in modo che sia più facile da confrontare, ovvero li porteremo a un denominatore comune:

Secondo la regola, di due numeri positivi, il numero maggiore è quello il cui modulo è maggiore. Quindi il numero razionale è maggiore di 0,(3) perché il modulo del numero è maggiore del modulo del numero 0,(3)

Ti è piaciuta la lezione?
Unisciti al nostro nuovo gruppo Vkontakte e inizia a ricevere notifiche di nuove lezioni

Quando si risolvono equazioni e disuguaglianze, nonché problemi con i moduli, è necessario individuare le radici trovate sulla retta reale. Come sapete, le radici trovate possono essere diverse. Possono essere così:, oppure possono essere così:,.

Di conseguenza, se i numeri non sono razionali ma irrazionali (se hai dimenticato di cosa si tratta, guarda nell'argomento) o sono espressioni matematiche complesse, posizionarli sulla linea dei numeri è molto problematico. Inoltre, le calcolatrici non possono essere utilizzate nell'esame e un calcolo approssimativo non garantisce al 100% che un numero sia inferiore a un altro (e se c'è una differenza tra i numeri confrontati?).

Naturalmente, sai che i numeri positivi sono sempre maggiori di quelli negativi e che se rappresentiamo un asse numerico, quando confrontiamo, numeri più grandi sarà posizionato a destra rispetto al più piccolo: ; ; eccetera.

Ma è sempre così facile? Dove segniamo sulla linea dei numeri.

Come confrontarli, ad esempio, con un numero? Ecco dove sta il problema...)

Per cominciare, parliamo in termini generali di come e cosa confrontare.

Importante: è auspicabile effettuare trasformazioni in modo tale che il segno di disuguaglianza non cambi! Cioè, nel corso delle trasformazioni, non è desiderabile moltiplicare per un numero negativo e è vietato quadrato se una delle parti è negativa.

Confronto frazioni

Quindi, dobbiamo confrontare due frazioni: e.

Ci sono diverse opzioni su come farlo.

Opzione 1. Porta le frazioni a un denominatore comune.

Scriviamola come frazione ordinaria:

- (come puoi vedere, ho anche ridotto del numeratore e denominatore).

Ora dobbiamo confrontare le frazioni:

Ora possiamo continuare a confrontare anche in due modi. Noi possiamo:

1. basta ridurre tutto a un denominatore comune, presentando entrambe le frazioni come improprie (il numeratore è maggiore del denominatore):

   Quale numero è maggiore? Esatto, quello il cui numeratore è maggiore, cioè il primo.

2. "scartare" (supponiamo di aver sottratto uno da ciascuna frazione e che il rapporto tra le frazioni, rispettivamente, non sia cambiato) e confronteremo le frazioni:

   Li portiamo anche a un denominatore comune:

   Abbiamo ottenuto esattamente lo stesso risultato del caso precedente: il primo numero è maggiore del secondo:

   Verifichiamo anche se ne abbiamo sottratto correttamente uno? Calcoliamo la differenza del numeratore nel primo calcolo e nel secondo:
   1)
   2)

Quindi, abbiamo esaminato come confrontare le frazioni, portandole a un denominatore comune. Passiamo a un altro metodo: confrontare le frazioni portandole a un comune ... numeratore.

Opzione 2. Confronto delle frazioni riducendo a un numeratore comune.

Si si. Questo non è un errore di battitura. A scuola, questo metodo viene insegnato raramente a qualcuno, ma molto spesso è molto conveniente. In modo che tu possa capire rapidamente la sua essenza, ti farò solo una domanda: "in quali casi il valore della frazione è il più grande?" Ovviamente dirai "quando il numeratore è il più grande possibile e il denominatore è il più piccolo possibile".

Ad esempio, lo dirai sicuramente Vero? E se dobbiamo confrontare tali frazioni: Penso che anche tu metterai subito correttamente il segno, perché nel primo caso sono divisi in parti, e nel secondo in intere, il che significa che nel secondo caso i pezzi sono molto piccoli, e di conseguenza: . Come puoi vedere, i denominatori sono diversi qui, ma i numeratori sono gli stessi. Tuttavia, per confrontare queste due frazioni, non è necessario trovare un denominatore comune. Anche se ... lo trovi e vedi se il segno di confronto è ancora sbagliato?

Ma il segno è lo stesso.

Torniamo al nostro compito originale: confrontare e. Confronteremo e Portiamo queste frazioni non a un denominatore comune, ma a un numeratore comune. Per questo è semplice numeratore e denominatore moltiplica la prima frazione per. Noi abbiamo:

E. Quale frazione è più grande? Esatto, il primo.

Opzione 3. Confronto delle frazioni mediante sottrazione.

Come confrontare le frazioni usando la sottrazione? Sì, molto semplice. Sottraiamo un altro da una frazione. Se il risultato è positivo, la prima frazione (ridotta) è maggiore della seconda (sottratta) e se negativa, viceversa.

Nel nostro caso, proviamo a sottrarre la prima frazione dalla seconda: .

Come hai già capito, traduciamo anche in una frazione ordinaria e otteniamo lo stesso risultato -. La nostra espressione diventa:

Inoltre, dobbiamo ancora ricorrere alla riduzione a un denominatore comune. La domanda è come: nel primo modo, convertendo le frazioni in quelle improprie, o nel secondo, come se si "rimuovesse" l'unità? A proposito, questa azione ha una giustificazione completamente matematica. Aspetto:

Mi piace di più la seconda opzione, poiché moltiplicare al numeratore quando si riduce a un denominatore comune diventa molte volte più facile.

Portiamo a un denominatore comune:

La cosa principale qui è non confondersi su quale numero e da dove abbiamo sottratto. Osserva attentamente il corso della soluzione e non confondere accidentalmente i segni. Abbiamo sottratto il primo dal secondo numero e ottenuto una risposta negativa, quindi?.. Esatto, il primo numero è maggiore del secondo.

Fatto? Prova a confrontare le frazioni:

Basta basta. Non abbiate fretta di portare a un denominatore comune o sottrarre. Guarda: può essere facilmente convertito in una frazione decimale. Quanto sarà? Destra. Cosa finisce per essere di più?

Questa è un'altra opzione: confrontare le frazioni riducendo a un decimale.

Opzione 4. Confronto delle frazioni usando la divisione.

Si si. E così è anche possibile. La logica è semplice: quando dividiamo un numero più grande per uno più piccolo, otteniamo un numero maggiore di uno nella risposta, e se dividiamo un numero più piccolo per uno più grande, la risposta cade nell'intervallo da a.

Per ricordare questa regola, prendine due a confronto numeri primi, per esempio, i. Sai cosa c'è di più? Ora dividiamo per. La nostra risposta è. Di conseguenza, la teoria è corretta. Se dividiamo per, ciò che otteniamo è inferiore a uno, il che a sua volta conferma ciò che in realtà è inferiore.

Proviamo ad applicare questa regola alle frazioni ordinarie. Confrontare:

Dividi la prima frazione per la seconda:

Riduciamo a poco a poco.

Il risultato è minore, quindi il dividendo è minore del divisore, ovvero:

Abbiamo analizzato tutte le possibili opzioni per confrontare le frazioni. Come puoi vedere ce ne sono 5:

• riduzione a un denominatore comune;
• riduzione a numeratore comune;
• riduzione alla forma di una frazione decimale;
• sottrazione;
• divisione.

Pronto per allenarti? Confronta le frazioni nel migliore dei modi:

Confrontiamo le risposte:

1. (- convertire in decimale)
2. (dividi una frazione per un'altra e riduci per numeratore e denominatore)
3. (selezionare la parte intera e confrontare le frazioni secondo il principio dello stesso numeratore)
4. (dividi una frazione per un'altra e riduci per numeratore e denominatore).

2. Confronto dei gradi

Ora immagina di dover confrontare non solo i numeri, ma anche le espressioni in cui c'è un grado ().

Certo, puoi facilmente mettere un segno:

Dopotutto, se sostituiamo il grado con la moltiplicazione, otteniamo:

Da questo piccolo e primitivo esempio, segue la regola:

Ora prova a confrontare quanto segue: . Puoi anche mettere facilmente un segno:

Perché se sostituiamo l'esponenziazione con la moltiplicazione...

In generale, capisci tutto e non è affatto difficile.

Le difficoltà sorgono solo quando, se confrontate, i gradi hanno basi e indicatori diversi. In questo caso, è necessario cercare di portare a una base comune. Per esempio:

Certo, sai che questo, di conseguenza, l'espressione assume la forma:

Apriamo le parentesi e confrontiamo cosa succede:

Un caso alquanto speciale è quando la base del grado() è minore di uno.

Se, quindi, di due gradi o più, quello il cui indicatore è minore.

Proviamo a dimostrare questa regola. Lascia stare.

Ve ne presentiamo alcuni numero naturale come differenza tra e.

Logico, non è vero?

Ora prestiamo attenzione alla condizione - .

Rispettivamente: . Di conseguenza, .

Per esempio:

Come capisci, abbiamo considerato il caso in cui le basi dei poteri sono uguali. Ora vediamo quando la base è nell'intervallo da a, ma gli esponenti sono uguali. Tutto è molto semplice qui.

Ricordiamo come confrontare questo con un esempio:

Ovviamente hai calcolato velocemente:

Pertanto, quando incontri problemi simili per il confronto, tieni a mente alcuni semplici esempi simili che puoi calcolare rapidamente e, sulla base di questo esempio, metti i segni in uno più complesso.

Quando esegui le trasformazioni, ricorda che se moltiplichi, aggiungi, sottrai o dividi, tutte le azioni devono essere eseguite su entrambi i lati sinistro e destro (se moltiplichi per, devi moltiplicare entrambi).

Inoltre, ci sono momenti in cui eseguire qualsiasi manipolazione non è semplicemente redditizio. Ad esempio, devi confrontare. IN questo caso, non è così difficile elevarsi a un potere, e disporre il segno in base a questo:

Facciamo un pò di pratica. Confronta i gradi:

Pronto a confrontare le risposte? Questo è quello che ho fatto:

1. - lo stesso di
2. - lo stesso di
3. - lo stesso di
4. - lo stesso di

3. Confronto di numeri con una radice

Cominciamo con cosa sono le radici? Ricordi questa voce?

La radice di un numero reale è un numero per il quale vale l'uguaglianza.

Radici grado dispari esistono per numeri negativi e positivi, e anche le radici- Solo per positivo.

Il valore della radice è spesso un decimale infinito, il che rende difficile calcolarlo con precisione, quindi è importante poter confrontare le radici.

Se hai dimenticato cos'è e con cosa si mangia -. Se ricordi tutto, impariamo a confrontare le radici passo dopo passo.

Diciamo che dobbiamo confrontare:

Per confrontare queste due radici, non è necessario fare alcun calcolo, basta analizzare il concetto stesso di "radice". Capito di cosa sto parlando? Sì, su questo: altrimenti può essere scritto come la terza potenza di un numero, uguale alla radice dell'espressione.

Cos'altro? o? Questo, ovviamente, puoi confrontare senza alcuna difficoltà. Maggiore è il numero che eleviamo a potenza, maggiore sarà il valore.

Così. Prendiamo la regola.

Se gli esponenti delle radici sono gli stessi (nel nostro caso, è così), è necessario confrontare le espressioni della radice (e) - maggiore è il numero della radice, maggiore è il valore della radice con indicatori uguali.

Difficile da ricordare? Quindi basta tenere a mente un esempio e. Quello di più?

Gli esponenti delle radici sono gli stessi, poiché la radice è quadrata. L'espressione radice di un numero () è maggiore di un altro (), il che significa che la regola è veramente vera.

Ma se le espressioni radicali fossero le stesse, ma i gradi delle radici fossero diversi? Per esempio: .

È anche abbastanza chiaro che estraendo una radice di grado maggiore, si otterrà un numero minore. Prendiamo ad esempio:

Denota il valore della prima radice come, e la seconda - come, quindi:

Puoi facilmente vedere che ci dovrebbe essere di più in queste equazioni, quindi:

Se le espressioni radice sono le stesse(nel nostro caso), e gli esponenti delle radici sono diversi(nel nostro caso, questo è e), allora è necessario confrontare gli esponenti(E) - maggiore è l'esponente, minore è l'espressione data.

Prova a confrontare le seguenti radici:

Confrontiamo i risultati?

Abbiamo affrontato con successo questo :). Sorge un'altra domanda: e se fossimo tutti diversi? E il grado, e l'espressione radicale? Non tutto è così difficile, dobbiamo solo "sbarazzarci" della radice. Si si. Sbarazzarsi di esso.)

Se abbiamo gradi ed espressioni radicali differenti, dobbiamo trovare il minimo comune multiplo (leggi la sezione relativa) per gli esponenti della radice ed elevare entrambe le espressioni a una potenza uguale al minimo comune multiplo.

Che siamo tutti a parole e a parole. Ecco un esempio:

1. Guardiamo gli indicatori delle radici - e. Il loro multiplo minimo comune è .
2. Alziamo entrambe le espressioni a una potenza:
3. Trasformiamo l'espressione ed espandiamo le parentesi (maggiori dettagli nel capitolo):
4. Consideriamo ciò che abbiamo fatto e mettiamo un segno:

4. Confronto di logaritmi

Quindi, lentamente ma inesorabilmente, ci siamo avvicinati alla questione di come confrontare i logaritmi. Se non ricordi che tipo di animale è questo, ti consiglio di leggere prima la teoria della sezione. Leggere? Quindi rispondi ad alcune domande importanti:

1. Qual è l'argomento del logaritmo e qual è la sua base?
2. Cosa determina se una funzione è crescente o decrescente?

Se ricordi tutto e lo hai imparato bene, iniziamo!

Per confrontare i logaritmi tra loro, devi conoscere solo 3 trucchi:

• riduzione alla stessa base;
• lanciare alla stessa argomentazione;
• confronto con il terzo numero.

Innanzitutto, presta attenzione alla base del logaritmo. Ricordi che se è minore, la funzione diminuisce e se è maggiore, aumenta. Questo è ciò su cui si baseranno i nostri giudizi.

Considerare di confrontare i logaritmi che sono già stati ridotti alla stessa base o argomento.

Per cominciare, semplifichiamo il problema: inseriamo i logaritmi confrontati pari basi. Quindi:

1. La funzione, quando cresce sull'intervallo da, significa, per definizione, poi (“confronto diretto”).
2. Esempio:- le basi sono le stesse, rispettivamente confrontiamo gli argomenti: , quindi:
3. La funzione, at, decresce sull'intervallo from, che significa, per definizione, quindi ("confronto inverso"). - le basi sono le stesse, rispettivamente confrontiamo gli argomenti: , invece, il segno dei logaritmi sarà “inverso”, poiché la funzione decresce: .

Consideriamo ora i casi in cui le basi sono diverse, ma gli argomenti sono gli stessi.

1. La base è più grande.
   • . In questo caso, utilizziamo il "confronto inverso". Ad esempio: - gli argomenti sono gli stessi, e. Confrontiamo le basi: però il segno dei logaritmi sarà “inverso”:
2. La base a è nel mezzo.
   • . In questo caso, utilizziamo il "confronto diretto". Per esempio:
   • . In questo caso, utilizziamo il "confronto inverso". Per esempio:

Scriviamo tutto in forma tabellare generale:

, in cui	, in cui

Di conseguenza, come hai già capito, quando confrontiamo i logaritmi, dobbiamo portare alla stessa base, o argomento, Arriviamo alla stessa base usando la formula per passare da una base all'altra.

Puoi anche confrontare i logaritmi con un terzo numero e, in base a questo, dedurre cosa è meno e cosa è più. Ad esempio, pensa a come confrontare questi due logaritmi?

Un piccolo suggerimento: per confronto, il logaritmo ti aiuterà molto, il cui argomento sarà uguale.

Pensiero? Decidiamo insieme.

Possiamo facilmente confrontare questi due logaritmi con te:

Non sai come? Vedi sopra. L'abbiamo appena smontato. Che segno ci sarà? Destra:

Concordare?

Confrontiamo tra loro:

Dovresti ottenere quanto segue:

Ora combina tutte le nostre conclusioni in una. È accaduto?

5. Confronto di espressioni trigonometriche.

Cos'è seno, coseno, tangente, cotangente? A cosa serve il cerchio unitario e come trovare il valore delle funzioni trigonometriche su di esso? Se non conosci le risposte a queste domande, ti consiglio vivamente di leggere la teoria su questo argomento. E se lo sai, confrontare le espressioni trigonometriche tra loro non è difficile per te!

Rinfreschiamoci un po' la memoria. Disegniamo un cerchio trigonometrico unitario e un triangolo inscritto in esso. Sei riuscito? Ora segna su quale lato abbiamo il coseno e su quale seno, usando i lati del triangolo. (Certo, ti ricordi che il seno è il rapporto tra il lato opposto all'ipotenusa e il coseno di quello adiacente?). Hai disegnato? Bene! Il tocco finale: scrivi dove lo avremo, dove e così via. Reprimere? Uff) Confronta quello che è successo tra me e te.

Uff! Ora iniziamo il confronto!

Supponiamo di dover confrontare e . Disegna questi angoli usando i suggerimenti nelle caselle (dove abbiamo segnato dove), disponendo i punti sul cerchio unitario. Sei riuscito? Questo è quello che ho fatto.

Ora abbassiamo la perpendicolare dai punti che abbiamo segnato sul cerchio all'asse... Quale? Quale asse mostra il valore dei seni? Destra, . Ecco cosa dovresti ottenere:

Guardando questa cifra, che è più grande: o? Naturalmente, perché il punto è al di sopra del punto.

Allo stesso modo, confrontiamo il valore dei coseni. Abbassiamo solo la perpendicolare sull'asse ... Giusto, . Di conseguenza, guardiamo in quale punto è a destra (bene, o più alto, come nel caso dei seni), quindi il valore è maggiore.

Probabilmente sai già come confrontare le tangenti, giusto? Tutto quello che devi sapere è cosa è tangente. Allora cos'è la tangente?) Esatto, il rapporto tra seno e coseno.

Per confrontare le tangenti, disegniamo anche un angolo, come nel caso precedente. Diciamo che dobbiamo confrontare:

Hai disegnato? Ora segniamo anche i valori del seno sull'asse delle coordinate. Notato? E ora indica i valori del coseno sulla linea delle coordinate. È accaduto? Confrontiamo:

Ora analizza ciò che hai scritto. - dividiamo un segmento grande in uno piccolo. La risposta sarà un valore esattamente maggiore di uno. Destra?

E quando dividiamo il piccolo per il grande. La risposta sarà un numero esattamente inferiore a uno.

Quindi il valore di quale espressione trigonometrica è maggiore?

Destra:

Come ora capisci, il confronto delle cotangenti è lo stesso, solo al contrario: osserviamo come i segmenti che definiscono coseno e seno si relazionano tra loro.

Prova a confrontare tu stesso le seguenti espressioni trigonometriche:

Esempi.

Risposte.

CONFRONTO DEI NUMERI. LIVELLO MEDIO.

Quale dei numeri è maggiore: o? La risposta è ovvia. E ora: o? Non è più così ovvio, giusto? E quindi: o?

Spesso è necessario sapere quale delle espressioni numeriche è maggiore. Ad esempio, quando si risolve una disuguaglianza, inserire i punti sull'asse nell'ordine corretto.

Ora ti insegnerò a confrontare tali numeri.

Se hai bisogno di confrontare i numeri e, metti un segno tra di loro (derivato dalla parola latina Versus o abbreviato vs. - contro):. Questo segno sostituisce il segno di disuguaglianza sconosciuto (). Inoltre, eseguiremo trasformazioni identiche fino a quando non sarà chiaro quale segno dovrebbe essere messo tra i numeri.

L'essenza del confronto dei numeri è la seguente: trattiamo il segno come se fosse una sorta di segno di disuguaglianza. E con l'espressione, possiamo fare tutto ciò che di solito facciamo con le disuguaglianze:

• aggiungi qualsiasi numero ad entrambe le parti (e sottrai, ovviamente, possiamo anche)
• "sposta tutto in una direzione", ovvero sottrai una delle espressioni confrontate da entrambe le parti. Al posto dell'espressione sottratta rimarranno: .
• moltiplicare o dividere per lo stesso numero. Se questo numero è negativo, il segno di disuguaglianza è invertito: .
• Alza entrambe le parti alla stessa potenza. Se questa potenza è pari, devi assicurarti che entrambe le parti abbiano lo stesso segno; se entrambe le parti sono positive, il segno non cambia quando è elevato a potenza, e se sono negative, allora cambia al contrario.
• prendi la radice dello stesso grado da entrambe le parti. Se estraiamo la radice di un grado pari, devi prima assicurarti che entrambe le espressioni non siano negative.
• ogni altra trasformazione equivalente.

Importante: è auspicabile effettuare trasformazioni in modo tale che il segno di disuguaglianza non cambi! Cioè, nel corso delle trasformazioni, non è desiderabile moltiplicare per un numero negativo ed è impossibile quadrare se una delle parti è negativa.

Diamo un'occhiata ad alcune situazioni tipiche.

1. Esponenziale.

Esempio.

Cosa c'è di più: o?

Soluzione.

Poiché entrambi i lati della disuguaglianza sono positivi, possiamo fare il quadrato per eliminare la radice:

Esempio.

Cosa c'è di più: o?

Soluzione.

Anche qui possiamo quadrare, ma questo ci aiuterà solo a sbarazzarci della radice quadrata. Qui è necessario elevarsi a tal punto che entrambe le radici scompaiano. Ciò significa che l'esponente di questo grado deve essere divisibile per entrambi (il grado della prima radice) e per. Questo numero è, quindi lo eleviamo alla esima potenza:

2. Moltiplicazione per il coniugato.

Esempio.

Cosa c'è di più: o?

Soluzione.

Moltiplica e dividi ogni differenza per la somma coniugata:

Ovviamente il denominatore a destra è maggiore del denominatore a sinistra. Pertanto, la frazione destra è minore della sinistra:

3. Sottrazione

Ricordiamolo.

Esempio.

Cosa c'è di più: o?

Soluzione.

Certo, potremmo piazzare tutto, raggruppare e piazzare di nuovo. Ma puoi fare qualcosa di più intelligente:

Si può vedere che ogni termine sul lato sinistro è minore di ogni termine sul lato destro.

Di conseguenza, la somma di tutti i termini sul lato sinistro è inferiore alla somma di tutti i termini sul lato destro.

Ma fa attenzione! Ci è stato chiesto di più...

Il lato destro è più grande.

Esempio.

Confronta i numeri e.

Soluzione.

Ricorda le formule trigonometriche:

Verifichiamo in quali quarti i punti e giacciono sul cerchio trigonometrico.

4. Divisione.

Anche qui usiamo una semplice regola: .

Con o, cioè.

Quando il segno cambia: .

Esempio.

Fai un confronto: .

Soluzione.

5. Confronta i numeri con il terzo numero

Se e, allora (legge di transitività).

Esempio.

Confrontare.

Soluzione.

Confrontiamo i numeri non tra loro, ma con il numero.

È ovvio che.

D'altro canto, .

Esempio.

Cosa c'è di più: o?

Soluzione.

Entrambi i numeri sono più grandi ma più piccoli. Scegli un numero tale che sia maggiore di uno ma minore dell'altro. Per esempio, . Controlliamo:

6. Cosa fare con i logaritmi?

Niente di speciale. Come sbarazzarsi dei logaritmi è descritto in dettaglio nell'argomento. Le regole di base sono:

\[(\log _a)x \vee b(\rm( )) \Leftrightarrow (\rm( ))\left[ (\begin(array)(*(20)(l))(x \vee (a^ b)\;(\rm(at))\;a > 1)\\(x \wedge (a^b)\;(\rm(at))\;0< a < 1}\end{array}} \right.\] или \[{\log _a}x \vee {\log _a}y{\rm{ }} \Leftrightarrow {\rm{ }}\left[ {\begin{array}{*{20}{l}}{x \vee y\;{\rm{при}}\;a >1)\\(x \cuneo y\;(\rm(at))\;0< a < 1}\end{array}} \right.\]

Possiamo anche aggiungere una regola sui logaritmi con basi diverse e lo stesso argomento:

Può essere spiegato come segue: più grande è la base, meno dovrà essere alzata per ottenere la stessa. Se la base è più piccola, allora è vero il contrario, poiché la funzione corrispondente è monotonicamente decrescente.

Esempio.

Confronta i numeri: i.

Soluzione.

Secondo le regole di cui sopra:

E ora la formula avanzata.

La regola per confrontare i logaritmi può anche essere scritta più breve:

Esempio.

Cosa c'è di più: o?

Soluzione.

Esempio.

Confronta quale dei numeri è maggiore: .

Soluzione.

CONFRONTO DEI NUMERI. IN BREVE SUL PRINCIPALE

1. Esponenziale

Se entrambi i lati della disuguaglianza sono positivi, possono essere quadrati per eliminare la radice

2. Moltiplicazione per il coniugato

Un coniugato è un moltiplicatore che integra l'espressione alla formula per la differenza dei quadrati: - coniuga per e viceversa, perché .

3. Sottrazione

4. Divisione

A o quello è

Quando il segno cambia:

5. Confronto con il terzo numero

Se e poi

6. Confronto di logaritmi

Regole di base:

Logaritmi con basi diverse e stesso argomento.

Argomento

Tipo di lezione

• studio e assimilazione primaria di nuovo materiale

Obiettivi della lezione

Piano di lezione

1. Introduzione.
2. Parte teorica
3. Parte pratica.
4. Compiti a casa.
5. Domande

introduzione

Vediamo video come ordinare i numeri negativi

Ora disponi i numeri negativi e decifra l'argomento della lezione:

Risposta: la parola "confronto".

Parte teorica

Confronto di numeri. regole

Quando si confrontano due numeri, la prima cosa da guardare sono i segni dei numeri che vengono confrontati. Un numero con un meno (negativo) è sempre minore di uno positivo.

Se entrambi i numeri confrontati hanno segni meno (negativi), allora dobbiamo confrontare i loro moduli, cioè confrontarli senza tener conto dei segni meno. Il numero il cui modulo risulta essere maggiore è in realtà minore.

Ad esempio -3 e -5. I numeri confrontati sono negativi. Quindi confrontiamo i loro moduli 3 e 5. 5 è maggiore di 3, quindi -5 è minore di -3.

Se uno dei numeri confrontati è zero, il numero negativo sarà minore di zero. (-3 < 0) E il positivo è di più. (3 > 0)

Puoi anche confrontare i numeri usando una linea di coordinate orizzontale. Il numero a sinistra è minore del numero a destra. Vale anche la regola opposta. Un punto con una coordinata più grande, sulla linea delle coordinate, è a destra di un punto con una coordinata più piccola.

Ad esempio, nella figura il punto E è a destra del punto A e la sua coordinata è maggiore. (5 > 1)

Confronto intero

Confronto di valori assoluti (moduli) di numeri

Disuguaglianze modulo

Parte pratica

Confronto di numeri su una linea numerica

Compiti

1. Spiega perché:
-5 meno di -1,
-2 su -16,
-25 è inferiore a 3,
0 più - 9.

2. Confronta:
i numeri sono visualizzati sulla linea delle coordinate: 0; ma; in; da. Confrontare:

1) a > 0; 2) dentro< 0; 3) 0 >da.
i numeri sono visualizzati sulla linea delle coordinate: 0; ma; in; da. Confrontali:

1) a > b; 2) con< а; 3) в < с.

3. Quale delle disuguaglianze è vera?
I numeri aeb sono negativi; | un | > | in |.
a) a > b; b) a< в.

4. Confronta il modulo dei numeri aeb.
I numeri aeb sono negativi; ma< в.

5. Quale delle disuguaglianze è vera?
a è un numero positivo
c è un numero negativo.
a) a > b; b) a< в?

6. Confronta:

Compiti a casa

1. Confronta i numeri

2. Calcola

3. Disporre i numeri in ordine crescente

Domande

Cosa mostra la coordinata di un punto su una retta?
Qual è il modulo di un numero da un punto di vista geometrico?
Qual è il modulo di un numero positivo?
Qual è il modulo di un numero negativo?
Qual è il modulo di zero?
Il valore assoluto di qualsiasi numero può essere negativo?
Qual è il numero opposto di 5?
Quale numero è il contrario di se stesso?

Produzione

Qualsiasi numero negativo è minore di qualsiasi numero positivo.

Di due numeri negativi, quello il cui modulo è maggiore è minore.

Zero è maggiore di qualsiasi numero negativo, ma minore di qualsiasi numero positivo.

Su una linea di coordinate orizzontali, un punto con una coordinata più grande si trova a destra di un punto con una coordinata più piccola.

Elenco delle fonti utilizzate

1. Enciclopedia matematica (in 5 volumi). - M.: Enciclopedia sovietica, 2002. - T. 1.
2. "L'ultima guida per gli scolari" "CASA XXI secolo" 2008
3. Riepilogo della lezione sull'argomento "Confronto dei numeri" Autore: Petrova V.P., insegnante di matematica (classi 5-9), Kiev
4. Nya Vilenkin, AS Chesnokov, SI Schwarzburd, VI Zhokhov, Matematica per il sesto anno, Libro di testo per il liceo

Lavorare sulla lezione
Pautinka AV
Petrova VP

Compilato e curato da AV Pautinka

Puoi porre una domanda sull'istruzione moderna, esprimere un'idea o risolvere un problema urgente a Forum Educazione dove un consiglio educativo di pensiero fresco e di azione si riunisce a livello internazionale. Avendo creato